生徒に教えるときは、出来るだけ興味を持たせ印象付けて教えたいものです。
子供が「すごーい」とか「面白ーい」などと、驚嘆しながら覚えたものは、なかなか忘れませんから。
そのためには教える側の知識や教え方が問われてきますね。
でも、理科や社会は興味を持たせやすいんですけど、算数ってなかなか難しいんですよね。
今回は、私の好きな「等差数列の和」の逸話から。
=======================
公差 d の等差数列の n 個の項 a1, a2, …, an の総和は
Sn=(a1+an)×n÷2
=======================
この公式を知らずに導き出したのは、なんと当時小学3年生だった少年ガウスでした。
(ガウスは18世紀のドイツの少年。 正確な記録では、この公式は13世紀にフィボナッチ数列で名を残しているフィボナッチさんの書にあるそうです。)
—————————–
ある時、算数の授業で1から100までの数字すべてを足すように課題を出されました。
子供たちは、当時ノート代わりの石板に 1+2=3、3+4=7、7+5=12、・・
と、面倒な計算を一生懸命取り組みはじめます。
先生は(早くても30分はかかるだろう)と思ってニンマリ腕組みをしていると、
間もなくガウス少年が、
「先生、できました」 と 手をあげました。
驚いた先生が、ガウス少年の石板を見ると、「5050」の正答が記されています。
「どうやって計算したんだ。先生だって、こんなに早く答えは出せないぞ。
最初から答えを知っていたんだろう。」
ガウス少年は口をとがらせて否定します。
彼は、みんなとは違った観点に注目して計算していたのです。
1+100=101、2+99=101、3+98=101… と全部101になるので答えは 101×50 = 5050
先生は、うなって感心した、というわけです。
—————————–
こんな話をしながら、「ガウスの公式」と教えると、子供たちも忘れません。
もちろん、
「台形の面積の公式と似ているよね。」という説明も忘れずに。
確かに「受験のための勉強」ではあるのですが、「学問は歴史的な知恵と知識の恩恵」であることも教えてあげたいですね。
ご家庭でも、お父さん、お母さんが工夫を凝らして独自に印象的な教え方をされていらっしゃる方もいるかと思います。 「こんな教え方が良かった」というものがありましたら、ぜひ真喜志にも教えてください。
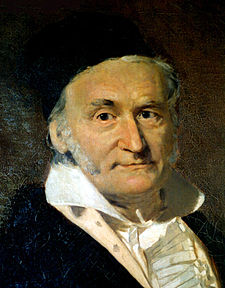
ヨハン・カール・フリードリヒ・ガウス






コメント
「三球儀」いいですねぇ。 そういうのが手軽に手に入る時代だったんですねぇ。
せっかくの三球儀ですから、ぜひ日食と月食もマスターされてくださいね。今年のヤマに含まれると思いますよ。
主人の勧めで「三球儀」を購入しました(笑)太陽、月、地球の自転と公転が一度に理解できます(算数ではなくて申し訳ありません)以後、月の満ち欠けの問題は全問正解です。でもその単元のみ。今年のヤマは月かな、と思っているのですがどうでしょう(笑)